On The Logical Probability Of The Truth Of Mathematical Theorems

I was reading through some of James Franklin’s papers on logical probability in an effort to not embarrass myself when I make my speech at the Broken Science Initiative event next weekend. It is from Franklin’s work, in part, that I learned probability.

My reasoning is thus: Given I often say stupid things when unprepared, the chance I say something stupid goes from near certain to something just under near certain if I prepare.

This, too, is an instance of logical probability, but one which is only partly quantifiable. Not all probability can be quantified. Stated a better way: probabilities can only be quantified in their conditions includes premises on quantification. We see another example at the end of this post.

Anyway, the paper of Franklin’s of interest is “Logical probability and the strength of mathematical conjectures.” Quoting:

How Can There Be Probabilistic Relations Between Necessary Truths?

There is a puzzle concerning how there could be probabilistic relations between the necessary truths of mathematics, the resolution of which shows something important about how logic works in mathematics. Suppose one argued: If e entails h, then P(h|e) is 1. But in mathematics, the typical case is that e does entail h, although that is perhaps as yet unknown. If, however, P(h|e) is really 1, how is it possible in the meantime to discuss the (nondeductive) support that e may give to h, that is, to treat P(h|e) as not equal to 1? In other words, if h and e are necessarily true or false, how can P(h|e) be other than 0 or 1?

Let’s see why this isn’t a problem for logical probability.

Take the fundamental theorem of calculus, which I believe many long-time readers know. But if you don’t know it, don’t sweat it. You’ll still be able to follow.

The “e” part of the evidence in Pr(h|e) is this (stealing from wokepedia):

Let f be a continuous real-valued function defined on a closed interval [a, b]. Let F be the function defined, for all x in [a, b], by

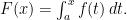
The “h” part is this (also stealing):

Then F is uniformly continuous on [a, b] and differentiable on the open interval (a, b), and

for all x in (a, b) so F is an antiderivative of f.

Anybody who had a first course in calculus knows Pr(h|e) = 1. Which is to say, we deduce h from e.

And right there is the problem. We do not derive “Pr(h|e) = 1”. That turns out to be a naughty and potentially misleading shorthand. There is nothing wrong with shorthand, of course, unless you don’t know the shorthand is shorthand. Mistaking shorthand for completeness and you’re in some deep kimchi.

Instead of directly knowing Pr(h|e), we instead augment e by a boatload of tacit and implicit premises, which look in part like this (again stealing):

All of that, and much more, is part of e. Those facts in the image are the tacit and implicit premises we didn’t (at first) write as part of e.

And these pictured are still only a portion of the premises we use. We also include things not easily written down, like logical steps moving from one part of the proof to the next, and the small jumps in math we make because they are “obvious”. They are all there, though. It’s just that they are used with varying degrees of ease.

Indeed, once you get good at these kinds of maneuvers it becomes easier and easier to forget that you made them. You become blind to them.

Yet they are all there, in e, or rather in what we should call “augmented e”. With that, anybody—who has the training, that is—can see Pr(h | augmented e) = 1. Whereas nobody can see, not without the augmentation, that Pr(h|e) = 1.

Of course, in mathematics, particularly for “larger” h, there is often more than one e that proves h. But that doesn’t change anything.

Now look how this works with an unproved conjecture (which Franklin also does) like the Riemann hypothesis, which is “the conjecture that the Riemann zeta function has its zeros only at the negative even integers and complex numbers with real part 1/2.” This is our new h.

Most mathematicians believe this h is true, but it is not yet proved in the same sense the calculus theorem above is. There are various e put forward in support of h, and those e with other non-deductive augmentations are why mathematicians think Pr(h | non-deductive augmented e) is high.

This “high” is not a number. So we end with yet another logical probability that is not quantified, and not even quantifiable, not unless we add more to our ” non-deductive augmented e”.

What would allow quantification? Something like this premise: “high means at least 90%.”

Subscribe or donate to support this site and its wholly independent host using credit card click here. For Zelle, use my email: matt@wmbriggs.com, and please include yours so I know who to thank.