This is an edited and expanded re-post from last September; it makes a natural and needed companion to last week’s series on how to statistically handle temperature time series, particularly Part V. This applies to the criticisms I made of BEST, the Bad Astronomer’s “deniers” column, and the practices of the often hyperbolic Michael Mann.
The example below is for predicting temperature via proxy, but it is just as valid for any statistical modeling example (marketing, medical, more). If you are familiar with the lingo and want to follow along for your own situation, the proxy are the X (the “independent” variables) and the temperature are the Y (the “dependent” variables). We want to predict Y as a function of X.
Suppose we are interested in temperature (in centigrade) for times which no direct measurements are available. Instead, at those times, we are able to measure a proxy. Perhaps this is a certain ratio of isotopes of some element, or it is the width of a tree ring, or whatever. We will use this proxy (X) to predict the (missing) temperature (Y).
First step: We must be able to measure both the temperature and the proxy simultaneously at some point in history. This is usually possible by finding a location where concurrent measurements of both exist. Here is a plot of what that might look like (this is a representative simulation).
The dots are the simultaneous measurements and the dashed line the result of a statistical model of proxy predicting temperature. This is a linear regression: but the exact model does not matter). It could have been a sine wave or include squared terms or whatever. Point is we have some Y = f(θ,X), Y is a function of X indexed on some unobservable parameters θ
Second step: we go to the location where no temperature measurements exist but where there are proxy measurements. Suppose one of these proxy values is, say, 122.89. The predicted temperature, via this model, was 19 centigrade. Get it? We need merely plug the values of the proxy into the model and out pop estimates of the temperatures. We can then use those estimated temperatures to make decisions of all kinds. Simple!
Except, of course, nobody believes that because the proxy was 122.89 the temperature was exactly, precisely 19oC. There is some uncertainty. The real temperature might have been, say, 19.2oC or 18.8oC, or some other value.
The classical way to express this uncertainty is to compute the parametric prediction interval. The 95% parametric prediction interval for this model happens to be 17.6oC to 20.4oC. The classical interpretation of this interval is screwy and tongue twisting. But we can use the Bayesian interpretation and say something like “There is a 95% chance the mean temperature was between 17.6oC and 20.4oC.” Since this interval is comfortably narrow, we go away secure in our estimate of temperature.
But we shouldn’t be confident, because that interval is far, far too narrow. The uncertainty of the actual temperature is vastly larger. Why? Take another look at what the interpretation of that interval is. What is a “mean temperature” and how is that different from plain old temperature?
It turns out that this interval is only about the unobservable parameter; it does not account for all the uncertainty that exists. Usually this “extra” uncertainty is just plain ignored1. But using (Bayesian) predictive methods, it is possible to account for and explain it easily (technically, we produce the posterior predictive distribution given the new data: see Part V).
If we use the (Bayesian) predictive method, the actual uncertainty of the temperature (and not parameters) is 9.6oC and 28.4oC. That’s nearly seven times more uncertain than the parameter-based way.
Did you see that? I’ll repeat it: the actual uncertainty is nearly seven times larger. This is because we are making a prediction of what the temperature was given the value of some proxy. This is why we want the uncertainty of the prediction. This picture shows the consequences:
The blue dots are the measurements of the proxy for which we had no concurrent temperatures. The black circles are a repeat of the original data (that the blue dots don’t span the range of the old data is just the result of the simulation). The narrow, dark-tan band in the center is the classical “parameter” interval for these new proxy measurements. The wide, light-tan band is the Bayesian posterior predictive distribution and represents the uncertainty of the actual temperature.
Notice that most of the old data points lie within the Bayesian interval—as we would hope they would—but very few of them lie within the classical parameter interval. The classical interval is shockingly narrow, and if relied upon guarantees, if not cockiness, then at least over-confidence.
These results were simulations, using a standard linear regression, but the lesson is the same for real data and regardless of what kind of statistical model is used (R code is here). The Bayesian predictive interval will always be wider.
But not wide enough! There are still some sources of uncertainty not accounted for. I have said above that the “actual” certainty was this-and-such. But that assumes the model I used was true. Is it? Who knows. There is thus more uncertainty in our model choice. Because of experience, we judge it likely that the model is not perfect; therefore the prediction intervals should be wider. How much wider is unknown: but they will be wider.
We assumed that the proxy and the temperature are measured without error of any kind. But if there is any measurement error, then the prediction intervals should be wider yet again. And there are a number of other peculiarities that apply just to temperature/proxy models, all of which were they fully accounted for push the prediction intervals wider.
Third step: Okay, we’ve sorted out the proper width of our uncertainty, taking into account all sources. Everybody’s happy. We now want to use our reconstructed temperatures. Perhaps as input to climate models, perhaps as input to models showing a change in something temperature related, like polar bear population or the extent of grasslands, or whatever. Or even as a raw plot, as BEST and Mann have done.
The raw plots from those organizations (we can now see) had “error bars”, i.e. the measurements of uncertainty, which were too narrow. Their plots (in part) were predictions of temperature given proxies (which included mixed sources of temperature measurements: again, see the series linked above). They therefore should have had the prediction intervals.
If the reconstructed temperatures are used as inputs to other models, what most people do is just plug the model guess with no uncertainty. That would be like plugging in 19oC plus-or-minus nothing, zero. There is no acknowledgement that the temperature that goes into these models is measured with error. What people should do is plug the range of temperatures in, and not just a point estimate. This isn’t easy to do: it’s not as simple as “plugging in”, but because it is difficult is no excuse not to do it.
If the range of uncertainty or temperature is not input, the resulting model will itself be too certain of itself. People will go off spouting that this or that change is “nearly certain” if temperature does this-or-that.
Here’s a contest: identify secondary studies which use reconstructed temperatures as input to models. The first one to find a study which uses the full predictive uncertainty of the reconstructed temperature wins.
Prediction: we will wait a long time before announcing a winner.
——————————————————————————————
1Click the “Start Here” at the top of the page and search out the teaching journal posts for a complete explanation why this is so.
Are you implying that when the temperature predictions are given in hundredths of a degree (two digits behind the decimal point), as I saw in a recent publication, this isn’t believable? I’m shocked. I thought all those thermometers and proxies measured to a hundredth of a degree.
Ray,
Yes, computers are wonderful things. But just to be clear: the above is a complete simulation and does not try to approximate any real data.
Great post Mr. Briggs! Any chance you could post how you calculated the Bayesian predictive interval?
Why would someone chose to use infilling (making up missing values) when building a model? In almost every case I’ve seen, “training” with infilled values reduces the model accuracy when tested against a validation set. Are there valid statistical reasons to do so?
Will,
This isn’t infilling. The blue dots are values of the proxy at places or times where no concurrent temperature exists.
I’ve actually painted a brighter picture than exists (though I make no claims for the representativeness of the example): it could be, and usually is, the case that new values of the Xs are outside the range of the old Xs.
Dr. Briggs,
I was making a (feeble?) joke about the phoney precision in the article on global warming where they show the result of their computations to a hundredth of a degree. When the calculated temperatures are given to a hundredth of a degree, you know it’s fake. Oops! I mean their certainty is too high.
Your narrow dark band is a confidence interval not a prediction interval. The classical prediction interval is much wider.
Well, Rob said it more briefly, but there are two classic intervals for a regression prediction, one for the mean and one for an individual value. The former multiplies the (estimated) variance by 1/n + dx^2/sum(dx^2), while the latter uses 1 + those terms. Your image looks like you are comparing those two. (The estimate of sigma^2 is still optimistic)
Mr. Briggs;
I understand that your example isn’t using infilling. I had assumed (too prematurely?) that the example model was to facilitate infilling. 🙂
Will,
There are those that believe an educated guess is better than no guess.
If you need to perform an FFT and feed it’s “fast time” output to a “slow time”
process like a Kalman filter – there are those that believe it is acceptable to
eliminate corrupt data and infill the gap with a linear interpolation in an attempt
to preserve as much valid information as possible.
FYI. The subject of determining when data is corrupt is why I keep checking this
site. I keep hoping the good doctor will provide some training for free!
Rob Hyndman,
Quite right; which is why I distinguished this one as the “parametric” interval, this being the one that almost all practitioners of statistics actually use.
Most—I mean nearly all—users of regression never consider that what they are doing is prediction. ANOVA tables of the parameters are examined, as are, perhaps, pictures of the parameter posterior distributions. But nearly none consider what the model actually means in terms of the “Y”s.
And even many (most) of those who are interested in prediction rarely use the wider intervals.
All,
I want to clarify that it is not so much a Bayes versus frequentist argument here, but a parameter-centric versus observables-centric philosophy I want to highlight. Prediction intervals like the Bayes one above exist, though I have never seen one used outside of a “forecasting” context. My view inverts this: I saw nearly all statistics is predictive, or should be viewed so.
The proxy-temperature example is a “forecast”, too.
Mr. Briggs: Thanks for the code.
Bill S: When you put it that way it sounds reasonable. But put a different way (like what I did here http://i55.tinypic.com/erlrer.jpg ) I have a hard time trusting in it. 🙂
Pingback: William M. Briggs, Statistician » What’s The Difference Between A Confidence Interval And A Credible Interval?
@Briggs, @Hyndman: What BEST, for example, actually calculates as its uncertainty is described as:
“We consider there to be two essential forms of quantifiable uncertainty in the Berkeley Earth averaging process:
“1. Statistical / Data-Driven Uncertainty: This is the error made in estimating the parameters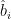
and Ì‚
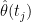due to the fact that the data, 
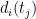, may not be an accurate reflection of the true temperature changes at location 
.
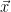2. Spatial Incompleteness Uncertainty: This is the expected error made in estimating the true land-surface average temperature due to the network of stations having incomplete coverage of all land areas.
“In addition, there is “structural†or “model-design†uncertainty, which describes the error a statistical model makes compared to the real-world due to the design of the model. Given that it is impossible to know absolute truth, model limitations are generally assessed by attempting to validate the underlying assumptions that a model makes and comparing those assumptions to other approaches used by different models. For example, we use a site reliability weighting procedure to reduce the impact of anomalous trends (such as those associated with urban heat islands), while other models (such as those developed by GISS) attempt to remove anomalous trends by applying various corrections. Such differences are an important aspect of model design. In general, it is impossible to directly quantify structural uncertainties, and so they are not a factor in our standard uncertainty model. However, one may be able to identify model limitations by drawing comparisons between the results of the Berkeley Average and the results of other groups. …”
The first point seems to be saying that they are looking at the uncertainty of parameters rather than predictions based on those parameters, which I believe is Briggs’ point. Their error bars thus appear to be more than confidence intervals, but less than prediction intervals (classical or Bayesian). (I say, “appear to be” because certainty on this is beyond my pay grade, as it were.)
Briggs: how would one go about including all of the uncertainty of the input in to a model?
For something that has conditional dependencies I would think trying a range of parameters at each stage of the model would be needed (monte Carlo at each “node” in the model).
For a simple model, would running the the model with the extremes be enough?
This is starting to sound more like modern game theory…
Will,
Well, you can take a look at the code to tease out some of it for this particular instance.
You have the right idea: running over the range of possibilities, taking into the account the chance of those possibilities.
It’s not easy! We’ll talk more about it in time.
Nice post. The graphic clearly displays why the uncertainty range for estimates of temperature derived from proxies must be wide (actually holds true for proxy derived estimates of just about anything.)
For example, if you look at a single vertical column of the graph, say around a value of 140 for the proxy, you see that the range of temperatures associated with proxy values of ~140 range from about 14 or 15 to 32 or 33. Assuming no measurement error, all of these are valid correlations between the proxy and temperature and if you are trying estimate temperature from a proxy value, you can’t know where in this range the true temperature value lies. Furthermore, you really can’t reduce the range of uncertainty much by gathering more data on the correlation of temperature and the proxy. It might be reduced a little if, by some chance, nearly all the new data points fell near the middle of the range, but not by much.
No I am not as certain how this applies to estimates of average global temperature but for proxy-based estimates of temperature, it clearly shows that you really need very tightly constrained correlations between temperature and the proxy for the estimates to have any meaning. There are few proxy-methods, such as some of the isotope-based methods on forams, where the correlation between temperature and the proxy have been laboratory-determined where the correlations seems relatively well-constrained, but for many methods (e.g., tree rings) the weak correlation and the wide-range of temperatures that correlate with a particular ring width in a given tree make them have very wide uncertainty intervals.
I think there are some steps missing. Take Mann’s tree rings for example, where the claim is that tree ring widths can be used as a proxy for temperature, despite comments from others that tree ring widths also depend upon a whole slew of other variables. Can a calibration done in modern times also be used in times long ago (and places far away)? Or take some other climate change advocates who use the proxies upside down and claim it doesn’t matter. Or consider those advocates who only use the proxies that give them the answer they were looking for.
As well as the Statistics bollocks, there’s also the Science bollocks. Thus when using the Yamal tree proxies, those climate scientists didn’t calibrate them versus local mean temperatures but versus global means*. By the standards common in the physical sciences, they are a notably dim bunch.
*Or perhaps it was Northern Hemisphere means, which is almost equally silly.